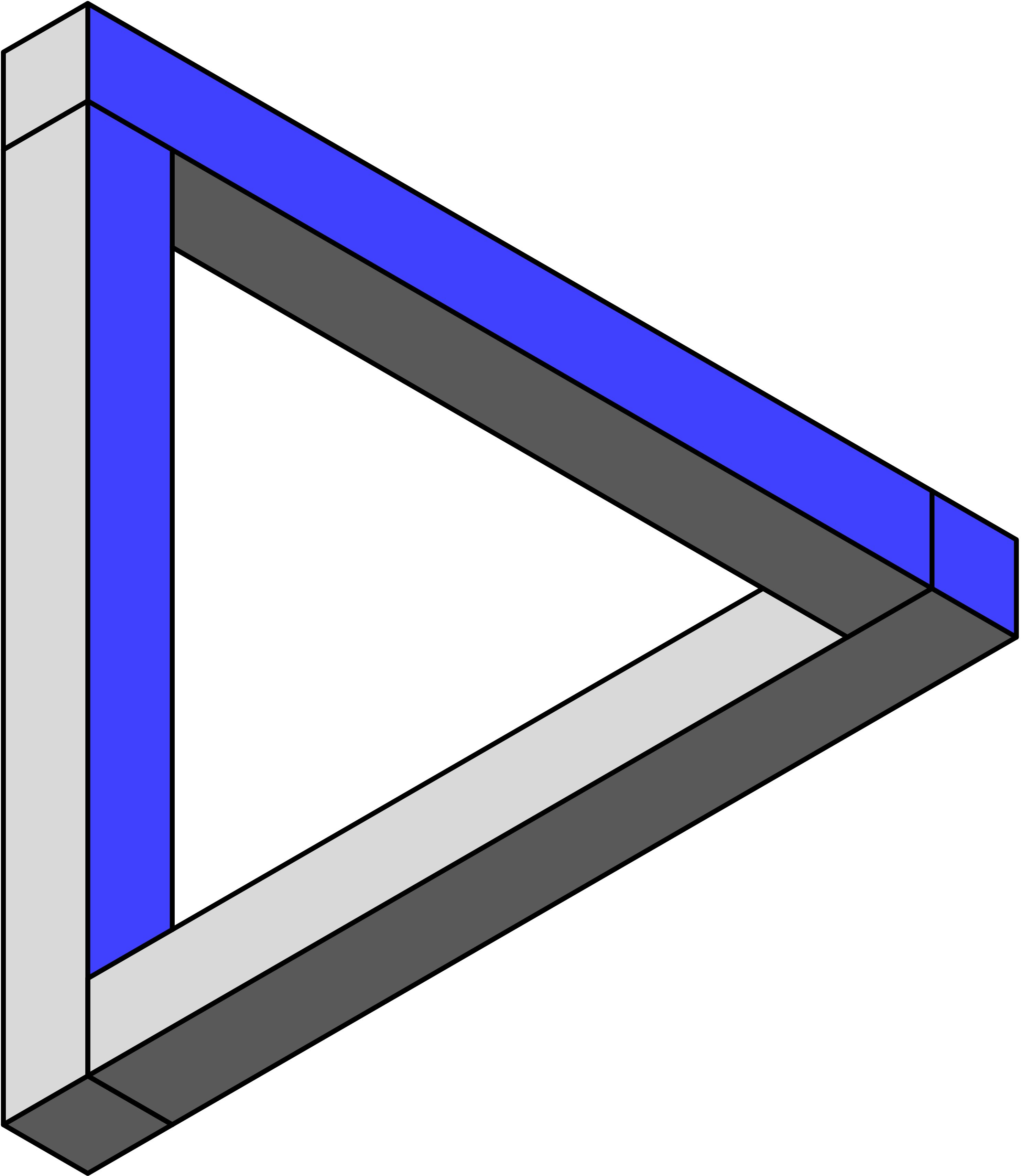
Triangle de Penrose

Auteur ou autrice : Yvon Henel.

Mise en ligne le 23 février 2023

Code

%%% figures impossibles
%%% Y. Henel 2004-02-22

%%% configuration
%%% vous pouvez changer les valeurs des variables ci-dessous


numeric u; u=10cm;

numeric long, larg; long=u; larg=.1u;  

numeric rotat; rotat:=30;

boolean avec_couleur;
%%% commentez l'une des deux égalités ci-dessous :
% avec_couleur=false;  % pas de couleur 
avec_couleur=true;    % de la couleur
%%% on peut redéfinir les couleurs ici :
color couleur[];
couleur1 = 0.35white; 
couleur2 = 0.85white;
couleur3 = 0.75blue+.25white;
%%%% fin de la partie configuration

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% constantes
%%% ne pas toucher !
pair V[], v[];

v1=dir 60; v2=dir(-60);
V1=long*v1; V3=larg*right; V2=larg*v2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


beginfig(1);
  z0=origin;        z1=z0 shifted V2;
  z2=z1 shifted V3; z3=z0 shifted V3;
  for i=0 upto 3:
    z[4+i] = z[i] shifted V1;
  endfor;
  z.aa = z2 shifted up;
  z.a= whatever[z2,z.aa]=whatever[z3,z7];
  z.b=z.a shifted right;
  z8= whatever[z.a,z.b]=whatever[z2,z6];
  numeric langle;
  langle= 180 - angle(z2-z3);  

  for i=0 upto 8:
    z[10+i] = z[i] rotatedabout(z0,rotat);
  endfor;
  for i=0 upto 8:
    z[20+i] = (z[10+i] rotatedabout(z13, langle)) shifted (z17-z13);
  endfor;
  for i=0 upto 8:
    z[30+i] = (z[10+i] rotatedabout(z13, 120)) shifted (z27-z13);
  endfor;

  if avec_couleur:
    for i=0 upto 8: z[40+i]=z[10+i]; z[50+i] = z[20+i]; endfor;
    for i=1 upto 3:
      fill z[10*i+16]--z[10*i+17]--z[10*i+6]--z[10*i+18]--cycle withcolor couleur[i];
      fill z[20+10*i]--z[20+10*i+3]--z[10*i]--z[10*i+1]--cycle withcolor couleur[i];
    endfor;
  fi

  pickup pencircle scaled .5mm;
  for k=1 upto 3:
    draw for j=0 upto 3: z[10*k+j]-- endfor cycle;
    draw z[10*k+4]--z[10*k+7]--z[10*k+6];
    for i=0, 3: draw z[10*k+i]--z[10*k+4+i]; endfor;
    draw z[10*k+6]--z[10*k+8];
  endfor;

% pendant la construction, repères :  
%  dotlabels(30,31,32,33,34,35,36,37,38);

endfig;

end