Illustration de la méthode de Newton
Auteur ou autrice : Vincent Zoonekynd.
Mise en ligne le 8 mai 2024
En 1999, puis mis à jour en 2001, Vincent Zoonekynd a mis en ligne un fichier MetaPost illustrant différentes utilisations du programme avec plus de 300 exemples. Ces exemples sont disponibles sur le CTAN.
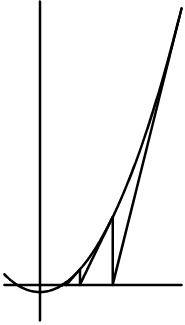
Ici, est illustré la méthode de Newton pour la résolution de $f(x)=0$.
Code
beginfig(128)
u := 5mm;
% vardef est nécessaire pour pouvoir passer f en argument
vardef f(expr x) = x**2 -.1 enddef;
def axes(expr xmin,xmax,ymin,ymax) =
draw ( (xmin,0) -- (xmax,0) ) scaled u;
draw ( (0,ymin) -- (0,ymax) ) scaled u;
enddef;
def courbe(suffix f)(expr xmin, xmax, M) =
draw ( ( xmin, f(xmin) )
for i=1 upto M:
-- ( xmin + (i/M)*(xmax - xmin), f( xmin + (i/M)*(xmax - xmin) ))
endfor ) scaled u;
enddef;
vardef newton(suffix f)(expr y, h, M) =
save x,t;
numeric x,t; x:=y;
for i=1 upto M:
t := x - f(x)/( (f(x+h) - f(x))/h );
draw ( (x,f(x)) -- (t,0) -- (t,f(t)) ) scaled u;
x := t;
endfor;
enddef;
axes(-.5,2,-.5,4);
courbe(f,-.5,2, 100);
newton(f, 2, .01, 10);
endfig;
end.
Mots clés : Newtonmathématiquesforaxeszoonekynd
Cet exemple fait partie de la collection d’exemples Exemples de Vincent Zoonekynd.