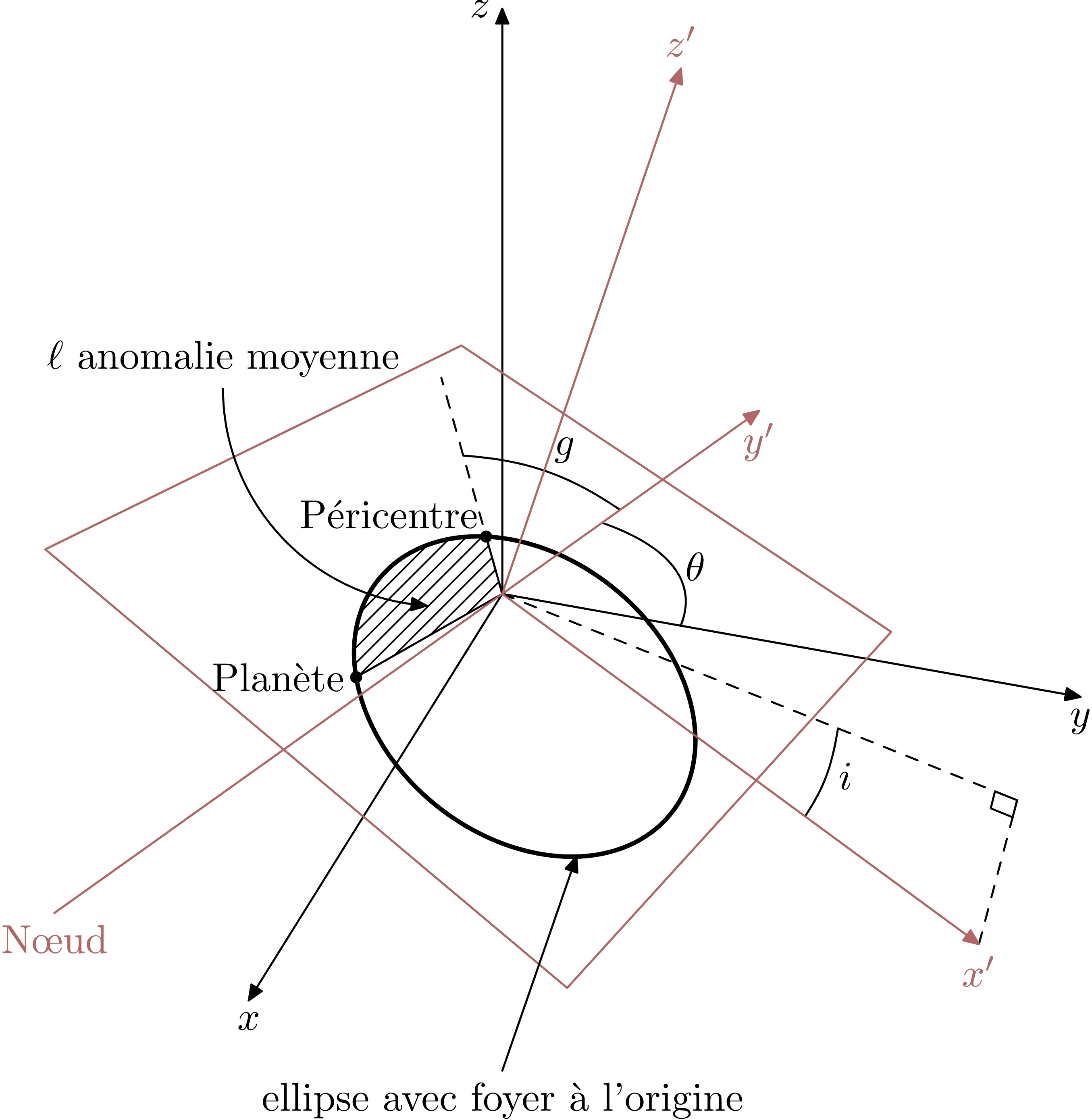
Orbite elliptique et son plan orbital
Auteur ou autrice : Maxime Chupin.
Mise en ligne le 17 janvier 2025
Cet exemple est un dessin classique de mécanique céleste. Il illustre la trajectoire elliptique d’une planète dans son plan. Les différents éléments importants qui caratérisent la trajectoire y sont représentés (inclinaison, nœud, anomalie, péricentre, etc.). Ce dessin provient d’un croquis de Jacques Féjoz.
Pour réaliser ce dessin, on a utilisé le package featpost présent sur le
CTAN. Ce package permet de réaliser des
dessins en trois dimensions (et en deux dimensions). Il est très pratique pour
illustrer de la géométrie basique dans l’espace.
Code
input featpost;
input latexmp;
input hatching;
beginfig(1);
% variable globales de vue 3D
% point de vue
f := (6,2,4);
% distance du plan de projection
Spread := 45;
% déclaration de variable
% les color sont soit des couleurs, soit des points 3D
color normal,u,v,u',v',pll,plr,pur,pul,O,I,J,K;
numeric projecplanesize;
path projecplanepath;
% Origine et repère initial
O = (0,0,0);
I = (1,0,0);
J = (0,1,0);
K = (0,0,1);
axesSize := 3;
orthaxes(axesSize,textext("$x$"),axesSize,textext("$y$"),axesSize,textext("$z$"));
% plan de l’ellipse
% trois vecteur de repère associés
normal = N((0.1,.3,1));
v = N( (-Y(normal), X(normal), 0) );
u = ncrossprod( v, normal );
projecplanesize = 1.7;
% les quatres points du plan pour le représenter
pll = projecplanesize*(-v-u);
plr = projecplanesize*(+v-u);
pur = projecplanesize*(+v+u);
pul = projecplanesize*(-v+u);
% on construit le cadre
projecplanepath = rp(pll)--rp(plr)--rp(pur)--rp(pul)--cycle;
color plancolor;
plancolor = (0.7,0.4,0.4);
draw projecplanepath withcolor plancolor;
% ellipse dans le plan
a:=1.1; b:=0.9; c:= sqrt(a**2-b**2);
% on fait une rotation autour de z' pour tourner l’ellipse dans le plan
rotangle := 140;
u'= rotvecaroundanother(rotangle,u,normal);
v'= rotvecaroundanother(rotangle,v,normal);
path ell,secteur;
color Ecentre, EA,EB;
% foyer à l’origine
Ecentre = -c*u';
EA = a*u';
EB = b*v';
% définition de l’ellipse par 3 vecteurs
% ellipticpath est déjà projeté
ell = ellipticpath(Ecentre,EA,EB);
% le secteur à hachurer
secteur := rp(O)--subpath (0,9) of ell -- cycle;
draw secteur;
% hachure
hatchfill secteur withcolor (45,1mm,-.4pt);
draw ell withpen pencircle scaled 1.1;
pair pericentre, planete;
pericentre = point 0 of ell;
planete = point 9 of ell;
dotlabel.ulft(textext("Péricentre"),pericentre);
dotlabel.lft(textext("Planète"),planete);
draw rp(O)--rp(2*u') dashed evenly;
angline(v,(a-c)*u',O,1.2,textext("$g$"),urt);
% le repère du plan
% inclinaison
draw rp(O)--rp(axesSize*(X(u),Y(u),0)) dashed evenly;
draw rp(axesSize*u)--rp(axesSize*(X(u),Y(u),0)) dashed evenly;
squareangline(O,axesSize*u,axesSize*(X(u),Y(u),0),0.1);
angline(axesSize*u,axesSize*(X(u),Y(u),0),O,2,textext("$i$"),rt);
drawarrow rp(O)--rp(axesSize*u) withcolor plancolor;
% Nœud
angline(axesSize*v,axesSize*J,O,1,textext("$\theta$"),rt);
drawoptions(withcolor plancolor);
drawarrow rp(-axesSize*v)--rp(axesSize*v);
% normal au plan
drawarrow rp(O)--rp(axesSize*normal);
label.bot(textext("$x'$"),rp(axesSize*u));
label.bot(textext("$y'$"),rp(axesSize*v));
label.top(textext("$z'$"),rp(axesSize*normal));
label.bot(textext("Nœud"),rp(-axesSize*v));
drawoptions();
% annotations
% anomalie
color anomalie,inEll;
anomalie = (1,-1,1.5);
inEll = -0.1a*u'+0.5*b*v';
label.top(textext("$\ell$ anomalie moyenne"),rp(anomalie));
drawarrow rp(anomalie){0,-1}..rp(inEll);
% ellipse
color annot;
pair P;
P = point 18 of ell;
annot = (3,1,0);
drawarrow rp(annot)..P;
label.bot(textext("ellipse avec foyer à l'origine"),rp(annot));
endfig;
end;
Mots clés : ellipseorbitemécanique céleste3Dangleplanfeatpostlatexmphatching