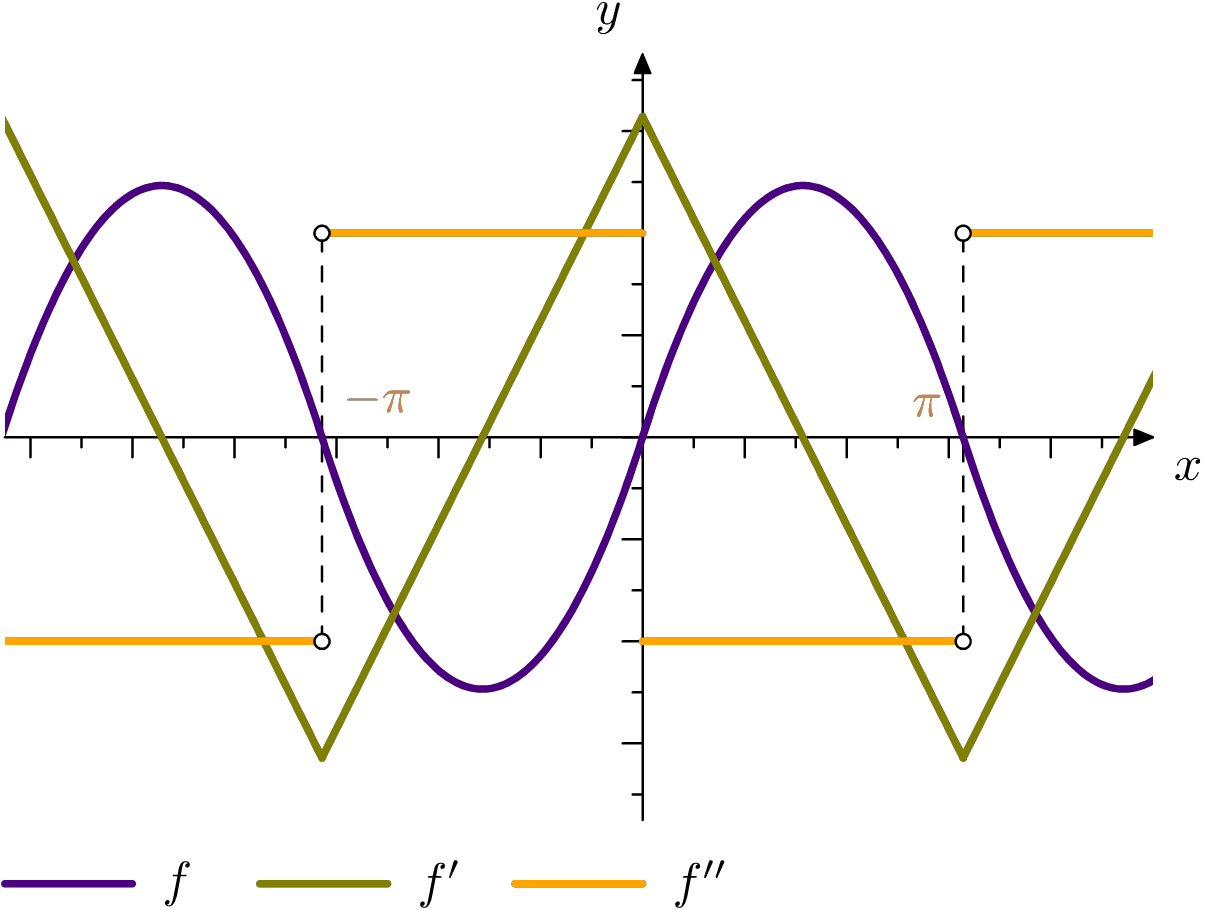
Une fonction et ses dérivées (mp-geom2d)
Auteur ou autrice : Jean-Michel Sarlat.
Mise en ligne le 19 mai 2025
mp-geom2d a été écrit avec le but de proposer des macros MetaPost permettant de réaliser une figure de géométrie en collant d’assez près à une description impérative :
- Soit $A$ le point de coordonnées $(2,3)$.
- Soit $B$ le point de coordonnées $(4,5)$.
- Trace la droite $(A,B)$.
- ...
Ici, on montre les exemples de la galerie de la documentation à la fois dans l’interface en français et celle en anglais.
Code
input geom2d;
labeloffset := 6;
gddU:=0.9cm;
vardef f(expr x) = x*(Pi-x) enddef; % f
vardef g(expr x) = Pi-2*x enddef; % f'
vardef h(expr x) = -2 enddef; % f''
beginfig(1);
Repere(9,6,5,3,.8,0.8);
Axes;
Debut;
Graduations;
trace (Pi,-2)--(Pi,2) dashed evenly;
trace (-Pi,-2)--(-Pi,2) dashed evenly;
trace Representation(f,0,Pi,100) avecCrayon(1.5,Indigo);
trace (Representation(f,0,Pi,100) scaled -1) avecCrayon(1.5,Indigo);
trace (Representation(f,0,Pi,100) shifted (-2*Pi,0)) avecCrayon(1.5,Indigo);
trace (Representation(f,0,Pi,100) scaled -1 shifted (2*Pi,0)) avecCrayon(1.5,Indigo);
trace Representation(g,0,Pi,100) avecCrayon(1.5,Olive);
trace (Representation(g,0,Pi,100) xscaled -1) avecCrayon(1.5,Olive);
trace (Representation(g,0,Pi,100) shifted (-2*Pi,0)) avecCrayon(1.5,Olive);
trace (Representation(g,0,Pi,100) xscaled -1 shifted (2*Pi,0)) avecCrayon(1.5,Olive);
trace Representation(h,0,Pi,100) avecCrayon(1.5,Orange);
trace (Representation(h,0,Pi,100) scaled -1) avecCrayon(1.5,Orange);
trace (Representation(h,0,Pi,100) shifted (-2*Pi,0)) avecCrayon(1.5,Orange);
trace (Representation(h,0,Pi,100) scaled -1 shifted (2*Pi,0)) avecCrayon(1.5,Orange);
pointe Point(Pi,2);
pointe Point(Pi,-2);
pointe Point(-Pi,2);
pointe Point(-Pi,-2);
label.urt(textext("\(-\pi\)"), (-Pi,0) gddEnPlace) withcolor Peru;
label.ulft(textext("\(\pi\)"), (Pi,0) gddEnPlace) withcolor Peru;
Fin;
trace (0,-0.5)--(1,-0.5) avecCrayon(1.5,Indigo);
label.rt(textext("\(f\)"), (1,-0.5) gddEnPlace);
trace (2,-0.5)--(3,-0.5) avecCrayon(1.5,Olive);
label.rt(textext("\(f'\)"), (3,-0.5) gddEnPlace);
trace (4,-0.5)--(5,-0.5) avecCrayon(1.5,Orange);
label.rt(textext("\(f''\)"), (5,-0.5) gddEnPlace);
endfig;
end
% %%% English version
input geom2d;
labeloffset := 6;
gddU:=0.9cm;
vardef f(expr x) = x*(Pi-x) enddef; % f
vardef g(expr x) = Pi-2*x enddef; % f'
vardef h(expr x) = -2 enddef; % f''
beginfig(1);
Frame(9,6,5,3,.8,0.8);
Axis;
gddBegin;
Graduations;
gddDraw (Pi,-2)--(Pi,2) dashed evenly;
gddDraw (-Pi,-2)--(-Pi,2) dashed evenly;
gddDraw Plot(f,0,Pi,100) withPen(1.5,Indigo);
gddDraw (Plot(f,0,Pi,100) scaled -1) withPen(1.5,Indigo);
gddDraw (Plot(f,0,Pi,100) shifted (-2*Pi,0)) withPen(1.5,Indigo);
gddDraw (Plot(f,0,Pi,100) scaled -1 shifted (2*Pi,0)) withPen(1.5,Indigo);
gddDraw Plot(g,0,Pi,100) withPen(1.5,Olive);
gddDraw (Plot(g,0,Pi,100) xscaled -1) withPen(1.5,Olive);
gddDraw (Plot(g,0,Pi,100) shifted (-2*Pi,0)) withPen(1.5,Olive);
gddDraw (Plot(g,0,Pi,100) xscaled -1 shifted (2*Pi,0)) withPen(1.5,Olive);
gddDraw Plot(h,0,Pi,100) withPen(1.5,Orange);
gddDraw (Plot(h,0,Pi,100) scaled -1) withPen(1.5,Orange);
gddDraw (Plot(h,0,Pi,100) shifted (-2*Pi,0)) withPen(1.5,Orange);
gddDraw (Plot(h,0,Pi,100) scaled -1 shifted (2*Pi,0)) withPen(1.5,Orange);
gddDrawPoint Point(Pi,2);
gddDrawPoint Point(Pi,-2);
gddDrawPoint Point(-Pi,2);
gddDrawPoint Point(-Pi,-2);
gddLabel.urt(textext("\(-\pi\)"), (-Pi,0)) withcolor Peru;
gddLabel.ulft(textext("\(\pi\)"), (Pi,0)) withcolor Peru;
gddEnd;
gddDraw (0,-0.5)--(1,-0.5) withPen(1.5,Indigo);
gddLabel.rt(textext("\(f\)"), (1,-0.5));
gddDraw (2,-0.5)--(3,-0.5) withPen(1.5,Olive);
gddLabel.rt(textext("\(f'\)"), (3,-0.5));
gddDraw (4,-0.5)--(5,-0.5) withPen(1.5,Orange);
gddLabel.rt(textext("\(f''\)"), (5,-0.5));
endfig;
end
Mots clés : géométriefonctiondérivéemp-geom2d
Cet exemple fait partie de la collection d’exemples Documentation de mp-geom2d