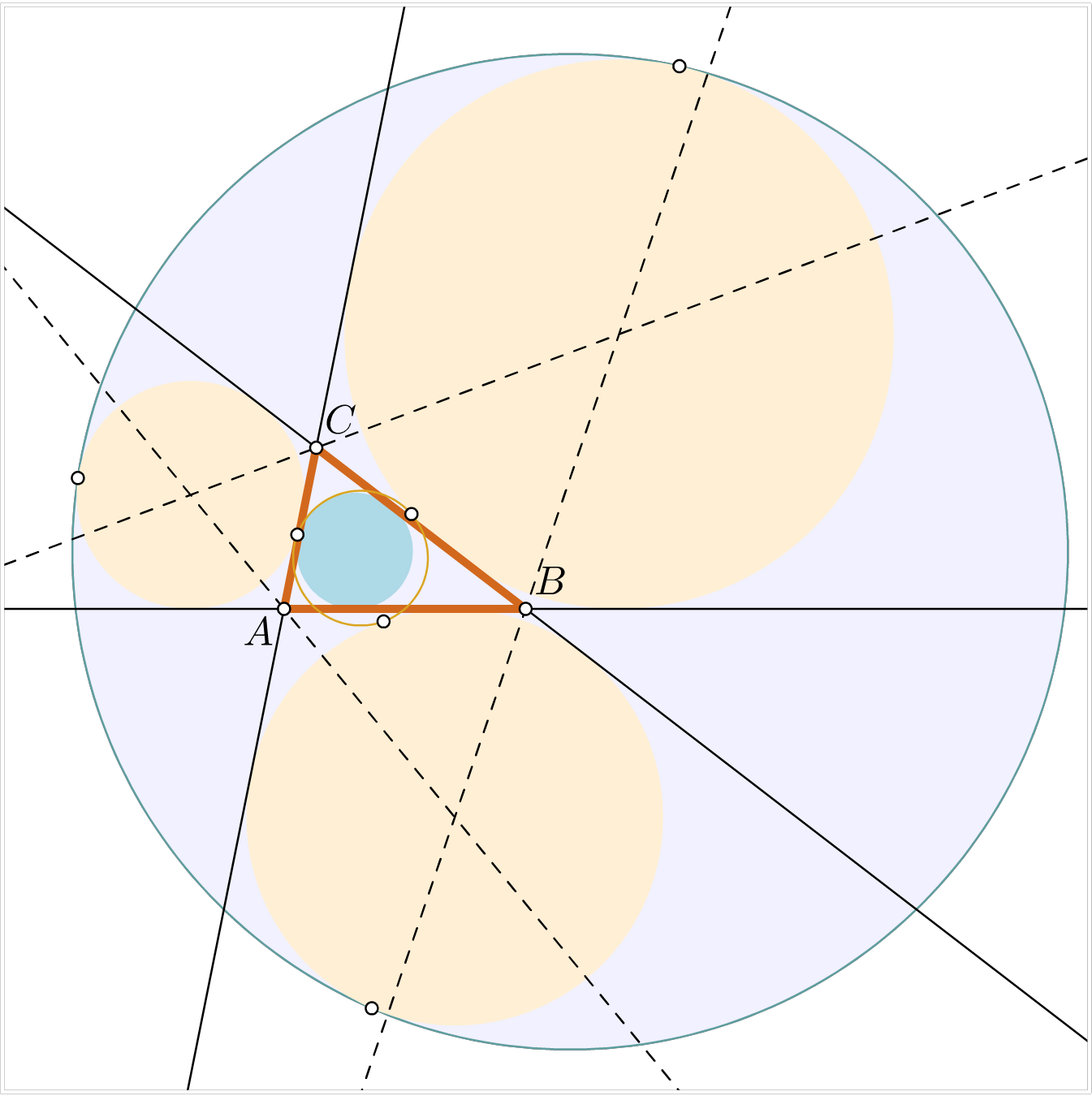
Cercle d’Apollonius d’un triangle (mp-geom2d)

Auteur ou autrice : Maxime Chupin.

Mise en ligne le 19 mai 2025

Code

input geom2d;
gddU:=0.35cm;
beginfig(1);
% nos trois points
A = Point(0,0);
B = Point(6,0);
C = Point(0.8,4);
T_ABC = Triangle(A,B,C);

C_I = CercleInscrit(T_ABC);
C_A = CercleExinscrit(T_ABC,2);
C_B = CercleExinscrit(T_ABC,3);
C_C = CercleExinscrit(T_ABC,1);

d_AB = Droite(A,B);
d_BC = Droite(B,C);
d_CA = Droite(C,A);

I = Centre(C_I);
I_C_A = Centre(C_A);
I_C_B = Centre(C_B);
I_C_C = Centre(C_C);
d_CAA = Droite(A,I_C_A);
d_CAB = Droite(B,I_C_B);
d_CAC = Droite(C,I_C_C);

A_S = AxeDeSimilitude(C_A,C_B,C_C);
P_CA = ProjectionPointSurDroite(I_C_A,A_S);
P_CB = ProjectionPointSurDroite(I_C_B,A_S);
P_CC = ProjectionPointSurDroite(I_C_C,A_S);

P_A = Inversion(P_CA,C_A);
P_B = Inversion(P_CB,C_B);
P_C = Inversion(P_CC,C_C);

C_R = CentreRadical(C_A,C_B,C_C);
% les neuf points pour les cercles d’euler (tangent intérieur)
% et d’apollonius (tangent extérieur)
D1 = Droite(C_R,P_A);
P1 = IntersectionDroiteCercle(D1,C_A,1);
Q1 = IntersectionDroiteCercle(D1,C_A,2);

D2 = Droite(C_R,P_B);
P2 = IntersectionDroiteCercle(D2,C_B,1);
Q2 = IntersectionDroiteCercle(D2,C_B,2);

D3 = Droite(C_R,P_C);
P3 = IntersectionDroiteCercle(D3,C_C,2);
Q3 = IntersectionDroiteCercle(D3,C_C,1);

% le cercle d’apollonius
Apol = CercleTroisPoints(P1,P2,P3);
colorie Apol withcolor 1.05*Lavender;
trace Apol withcolor CadetBlue;

% cercle inscrit
colorie C_I withcolor LightBlue;
% cercles exinscrits
colorie C_A withcolor PapayaWhip;
colorie C_B withcolor PapayaWhip;
colorie C_C withcolor PapayaWhip;

trace d_AB;
trace d_BC;
trace d_CA;

trace d_CAA dashed evenly;
trace d_CAB dashed evenly;
trace d_CAC dashed evenly;

trace T_ABC withpen pencircle scaled 2 withcolor  Chocolate;

C_E = CercleEuler(T_ABC);
trace C_E withcolor Goldenrod;

pointe P1;
pointe P2;
pointe P3;

pointe Q1;
pointe Q2;
pointe Q3;


marque.llft "A";
marque.urt "B";
marque.urt "C";
Fenetre(-7,-12,20,15)
endfig;
end.

%%%%% English version

input geom2d;
gddU:=0.35cm;
beginfig(1);

A = Point(0,0);
B = Point(6,0);
C = Point(0.8,4);
T_ABC = Triangle(A,B,C);

C_I = InscribedCircle(T_ABC);
C_A = EscribedCircle(T_ABC,2);
C_B = EscribedCircle(T_ABC,3);
C_C = EscribedCircle(T_ABC,1);

d_AB = Line(A,B);
d_BC = Line(B,C);
d_CA = Line(C,A);

I = Center(C_I);
I_C_A = Center(C_A);
I_C_B = Center(C_B);
I_C_C = Center(C_C);
d_CAA = Line(A,I_C_A);
d_CAB = Line(B,I_C_B);
d_CAC = Line(C,I_C_C);

A_S = AxisOfSimilitude(C_A,C_B,C_C);
P_CA = PointOnLineProjection(I_C_A,A_S);
P_CB = PointOnLineProjection(I_C_B,A_S);
P_CC = PointOnLineProjection(I_C_C,A_S);

P_A = Inverse(P_CA,C_A);
P_B = Inverse(P_CB,C_B);
P_C = Inverse(P_CC,C_C);

C_R = RadicalCenter(C_A,C_B,C_C);
% les neuf points pour les cercles d’euler (tangent intérieur)
% et d’apollonius (tangent extérieur)
D1 = Line(C_R,P_A);
P1 = LineCircleIntersection(D1,C_A,1);
Q1 = LineCircleIntersection(D1,C_A,2);

D2 = Line(C_R,P_B);
P2 = LineCircleIntersection(D2,C_B,1);
Q2 = LineCircleIntersection(D2,C_B,2);

D3 = Line(C_R,P_C);
P3 = LineCircleIntersection(D3,C_C,2);
Q3 = LineCircleIntersection(D3,C_C,1);

% le cercle d’apollonius
Apol = CircleThreePoints(P1,P2,P3);
gddFill Apol withcolor 1.05*Lavender;
gddDraw Apol withcolor CadetBlue;

% cercle inscrit
gddFill C_I withcolor LightBlue;
% cercles exinscrits
gddFill C_A withcolor PapayaWhip;
gddFill C_B withcolor PapayaWhip;
gddFill C_C withcolor PapayaWhip;

gddDraw d_AB;
gddDraw d_BC;
gddDraw d_CA;

gddDraw d_CAA dashed evenly;
gddDraw d_CAB dashed evenly;
gddDraw d_CAC dashed evenly;

gddDraw T_ABC withpen pencircle scaled 2 withcolor  Chocolate;

C_E = EulerCircle(T_ABC);
gddDraw C_E withcolor Goldenrod;

gddDrawPoint P1;
gddDrawPoint P2;
gddDrawPoint P3;

gddDrawPoint Q1;
gddDrawPoint Q2;
gddDrawPoint Q3;


gddMark.llft "A";
gddMark.urt "B";
gddMark.urt "C";
Window(-7,-12,20,15)
endfig;
end.