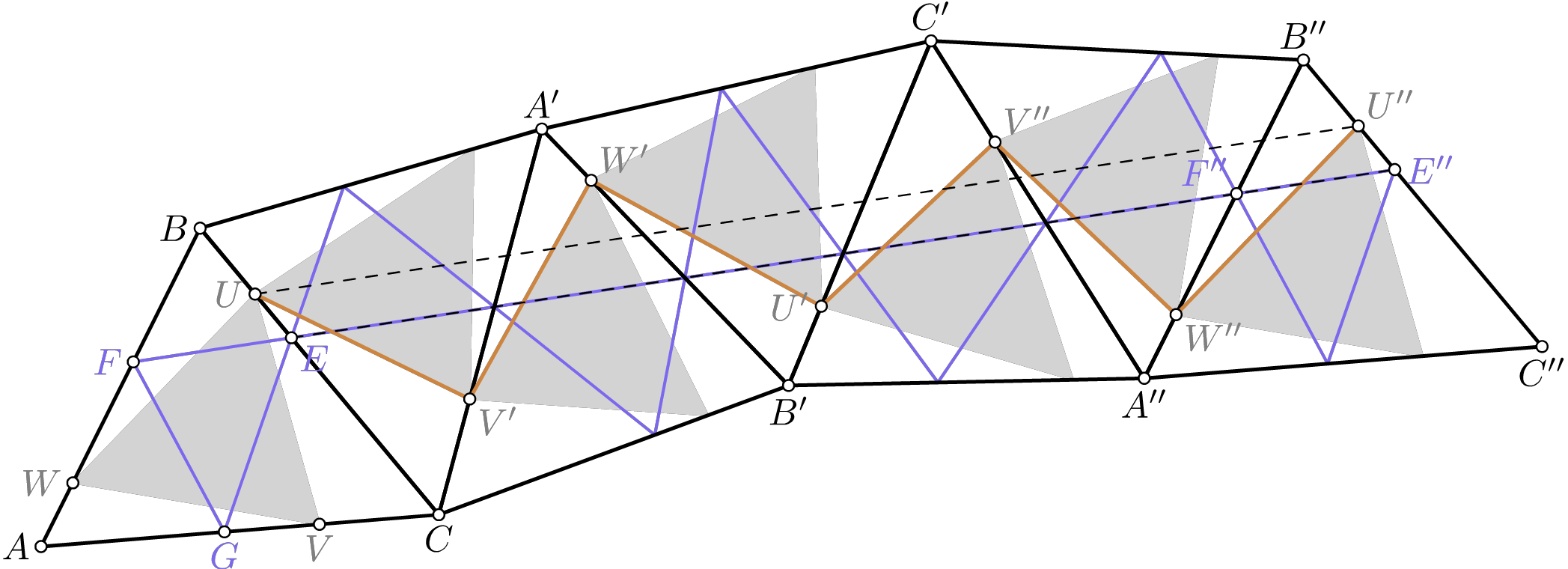
Triangle orthique et problème de Fagnano (mp-geom2d)

Auteur ou autrice : Maxime Chupin.

Mise en ligne le 19 mai 2025

Code

input geom2d;
gddU:=1.5cm;
beginfig(1);
numeric A[],B[],C[],E[],F[],G[],U[],W[],V[],T[],R[],P[];
A[1] = Point(0,0);
B1 = Point(1,2);
C1 = Point(2.5,0.2);
W1 = PointDe(Segment(A1,B1),0.2);
U1 = PointDe(Segment(B1,C1),0.23);
V1 = PointDe(Segment(C1,A1),0.3);
G1 = ProjectionPointSurDroite(B1,Droite(A1,C1));
F1 = ProjectionPointSurDroite(C1,Droite(A1,B1));
E1 = ProjectionPointSurDroite(A1,Droite(B1,C1));



for i:=0 step 3 until 3:

D[1+i] = Droite(B[1+i],C[1+i]);
A[2+i] = SymetrieAxiale(A[1+i],D[1+i]);

B[2+i] = B[1+i];
C[2+i] = C[1+i];

W[2+i] = SymetrieAxiale(W[1+i],D[1+i]);
V[2+i] = SymetrieAxiale(V[1+i],D[1+i]);
U[2+i] = U[1+i];

G[2+i] = SymetrieAxiale(G[1+i],D[1+i]);
F[2+i] = SymetrieAxiale(F[1+i],D[1+i]);
E[2+i] = E[1+i];

D[2+i] = Droite(A[2+i],C[2+i]);
B[3+i] = SymetrieAxiale(B[2+i],D[2+i]);
A[3+i] = A[2+i];
C[3+i] = C[2+i];
W[3+i] = SymetrieAxiale(W[2+i],D[2+i]);
U[3+i] = SymetrieAxiale(U[2+i],D[2+i]);
V[3+i] = V[2+i];
E[3+i] = SymetrieAxiale(E[2+i],D[2+i]);
F[3+i] = SymetrieAxiale(F[2+i],D[2+i]);
G[3+i] = G[2+i];

D[3+i] = Droite(A[3+i],B[3+i]);
C[4+i] = SymetrieAxiale(C[3+i],D[3+i]);
A[4+i] = A[3+i];
B[4+i] = B[3+i];
U[4+i] = SymetrieAxiale(U[3+i],D[3+i]);
V[4+i] = SymetrieAxiale(V[3+i],D[3+i]);
W[4+i] = W[3+i];
E[4+i] = SymetrieAxiale(E[3+i],D[3+i]);
G[4+i] = SymetrieAxiale(G[3+i],D[3+i]);
F[4+i] = F[3+i];
endfor;

for i:=1 upto 7:
    T[i] = Triangle(A[i],B[i],C[i]);
    Q[i] = Triangle(U[i],V[i],W[i]);
    P[i] = Triangle(E[i],F[i],G[i]);
    colorie Q[i] avecCrayon(0.5,LightGray);
    trace P[i] avecCrayon(0.8,MediumSlateBlue);
endfor;
for i:=1 upto 7:
    trace T[i] avecCrayon(1,black);
endfor;

trace LigneBrisee(U1,V2,W3,U4,V5,W6,U7) avecCrayon(1,Peru) ;
trace Segment(U1,U7) dashed evenly;
trace Segment(E1,E7) dashed evenly;
pointe A1; pointe B1; pointe C1;
pointe A2; pointe B3; pointe C4;
pointe A5; pointe B6; pointe C7;
gddLabel.lft(textext("$A$"),A1);
gddLabel.lft(textext("$B$"),B1);
gddLabel.bot(textext("$C$"),C1);
gddLabel.top(textext("$A'$"),A2);
gddLabel.bot(textext("$B'$"),B3);
gddLabel.top(textext("$C'$"),C4);
gddLabel.bot(textext("$A''$"),A5);
gddLabel.top(textext("$B''$"),B7);
gddLabel.bot(textext("$C''$"),C7);

pointe U1; pointe V1; pointe W1;
gddLabel.lft(textext("$U$"),U1) withcolor Gray;
gddLabel.bot(textext("$V$"),V1) withcolor Gray;
gddLabel.lft(textext("$W$"),W1) withcolor Gray;

gddLabel.lft(textext("$U'$"),U4) withcolor Gray;
gddLabel.lrt(textext("$V'$"),V2) withcolor Gray;
gddLabel.urt(textext("$W'$"),W3) withcolor Gray;
gddLabel.urt(textext("$U''$"),U7) withcolor Gray;
gddLabel.urt(textext("$V''$"),V5) withcolor Gray;
gddLabel.lrt(textext("$W''$"),W7) withcolor Gray;
pointe U4; pointe V2; pointe W3; 
pointe U7; pointe V5; pointe W7;
pointe E1; pointe F1; pointe G1;
gddLabel.lrt(textext("$E$"),E1) withcolor MediumSlateBlue;
gddLabel.lft(textext("$F$"),F1) withcolor MediumSlateBlue;
gddLabel.bot(textext("$G$"),G1) withcolor MediumSlateBlue;

gddLabel.ulft(textext("$F''$"),F7) withcolor MediumSlateBlue;
pointe F7;
gddLabel.rt(textext("$E''$"),E7) withcolor MediumSlateBlue;
pointe E7;
endfig;
end.

%%% English version

input geom2d;
gddU:=1.5cm;
beginfig(1);
numeric A[],B[],C[],E[],F[],G[],U[],W[],V[],T[],R[],P[];
A[1] = Point(0,0);
B1 = Point(1,2);
C1 = Point(2.5,0.2);
W1 = PointOf(Segment(A1,B1),0.2);
U1 = PointOf(Segment(B1,C1),0.23);
V1 = PointOf(Segment(C1,A1),0.3);
G1 = PointOnLineProjection(B1,Line(A1,C1));
F1 = PointOnLineProjection(C1,Line(A1,B1));
E1 = PointOnLineProjection(A1,Line(B1,C1));



for i:=0 step 3 until 3:

D[1+i] = Line(B[1+i],C[1+i]);
A[2+i] = AxialSymmetry(A[1+i],D[1+i]);

B[2+i] = B[1+i];
C[2+i] = C[1+i];

W[2+i] = AxialSymmetry(W[1+i],D[1+i]);
V[2+i] = AxialSymmetry(V[1+i],D[1+i]);
U[2+i] = U[1+i];

G[2+i] = AxialSymmetry(G[1+i],D[1+i]);
F[2+i] = AxialSymmetry(F[1+i],D[1+i]);
E[2+i] = E[1+i];

D[2+i] = Line(A[2+i],C[2+i]);
B[3+i] = AxialSymmetry(B[2+i],D[2+i]);
A[3+i] = A[2+i];
C[3+i] = C[2+i];
W[3+i] = AxialSymmetry(W[2+i],D[2+i]);
U[3+i] = AxialSymmetry(U[2+i],D[2+i]);
V[3+i] = V[2+i];
E[3+i] = AxialSymmetry(E[2+i],D[2+i]);
F[3+i] = AxialSymmetry(F[2+i],D[2+i]);
G[3+i] = G[2+i];

D[3+i] = Line(A[3+i],B[3+i]);
C[4+i] = AxialSymmetry(C[3+i],D[3+i]);
A[4+i] = A[3+i];
B[4+i] = B[3+i];
U[4+i] = AxialSymmetry(U[3+i],D[3+i]);
V[4+i] = AxialSymmetry(V[3+i],D[3+i]);
W[4+i] = W[3+i];
E[4+i] = AxialSymmetry(E[3+i],D[3+i]);
G[4+i] = AxialSymmetry(G[3+i],D[3+i]);
F[4+i] = F[3+i];
endfor;

for i:=1 upto 7:
    T[i] = Triangle(A[i],B[i],C[i]);
    Q[i] = Triangle(U[i],V[i],W[i]);
    P[i] = Triangle(E[i],F[i],G[i]);
    gddFill Q[i] withPen(0.5,LightGray);
    gddDraw P[i] withPen(0.8,MediumSlateBlue);
endfor;
for i:=1 upto 7:
    gddDraw T[i] withPen(1,black);
endfor;

gddDraw Polyline(U1,V2,W3,U4,V5,W6,U7) withPen(1,Peru) ;
gddDraw Segment(U1,U7) dashed evenly;
gddDraw Segment(E1,E7) dashed evenly;
gddDrawPoint A1; gddDrawPoint B1; gddDrawPoint C1;
gddDrawPoint A2; gddDrawPoint B3; gddDrawPoint C4;
gddDrawPoint A5; gddDrawPoint B6; gddDrawPoint C7;
gddLabel.lft(textext("$A$"),A1);
gddLabel.lft(textext("$B$"),B1);
gddLabel.bot(textext("$C$"),C1);
gddLabel.top(textext("$A'$"),A2);
gddLabel.bot(textext("$B'$"),B3);
gddLabel.top(textext("$C'$"),C4);
gddLabel.bot(textext("$A''$"),A5);
gddLabel.top(textext("$B''$"),B7);
gddLabel.bot(textext("$C''$"),C7);

gddDrawPoint U1; gddDrawPoint V1; gddDrawPoint W1;
gddLabel.lft(textext("$U$"),U1) withcolor Gray;
gddLabel.bot(textext("$V$"),V1) withcolor Gray;
gddLabel.lft(textext("$W$"),W1) withcolor Gray;

gddLabel.lft(textext("$U'$"),U4) withcolor Gray;
gddLabel.lrt(textext("$V'$"),V2) withcolor Gray;
gddLabel.urt(textext("$W'$"),W3) withcolor Gray;
gddLabel.urt(textext("$U''$"),U7) withcolor Gray;
gddLabel.urt(textext("$V''$"),V5) withcolor Gray;
gddLabel.lrt(textext("$W''$"),W7) withcolor Gray;
gddDrawPoint U4; gddDrawPoint V2; gddDrawPoint W3; 
gddDrawPoint U7; gddDrawPoint V5; gddDrawPoint W7;
gddDrawPoint E1; gddDrawPoint F1; gddDrawPoint G1;
gddLabel.lrt(textext("$E$"),E1) withcolor MediumSlateBlue;
gddLabel.lft(textext("$F$"),F1) withcolor MediumSlateBlue;
gddLabel.bot(textext("$G$"),G1) withcolor MediumSlateBlue;

gddLabel.ulft(textext("$F''$"),F7) withcolor MediumSlateBlue;
gddDrawPoint F7;
gddLabel.rt(textext("$E''$"),E7) withcolor MediumSlateBlue;
gddDrawPoint E7;
endfig;
end.