Trisectrices de l’angle droit au compas et à la règle
Auteur ou autrice : Maxime Chupin.
Mise en ligne le 18 octobre 2025
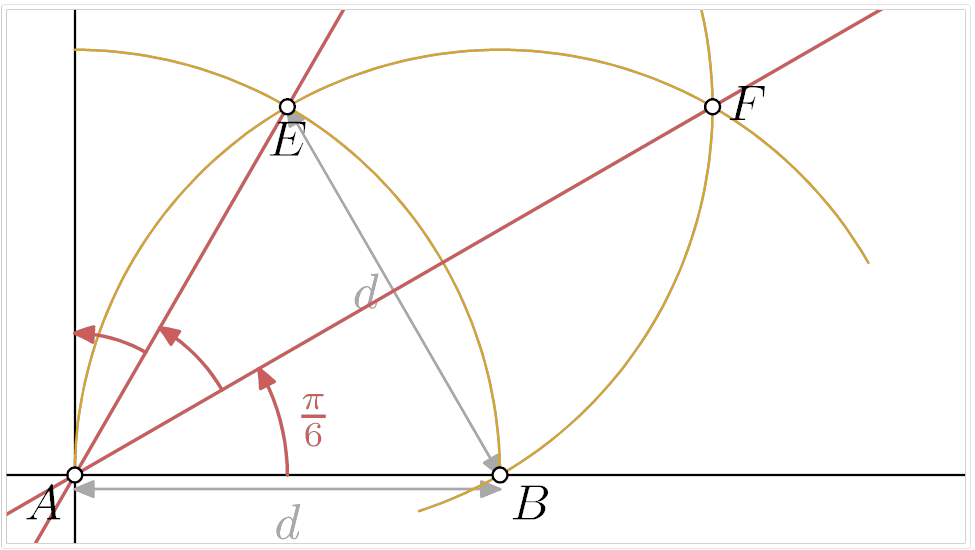
Soit $A$ un point duquel sont issues deux droites, respectivement horizontale et
verticale. Soit $d$ une certaine distance. En traçant le cercle de rayon $d$ et
de centre $A$, on obtient le point $B$ comme intersection de celui-ci avec la
droite horizontale. On trace ensuite le cercle de rayon $d$ et de centre $B$,
pour obtenir le point $E$ comme intersection des deux cercles jusque-là tracés.
Pour finir, on trace le cercle de rayon $d$ et de centre $E$ pour obtenir le
point $F$ comme intersection des deux derniers cercles tracés. Alors, on a les
angles suivants :
$$\widehat{BAF}=\widehat{FAE}=\frac{\pi}{6}.$$
Code
input geom2d;
def doublefleche expr p =
if path p or picture p: drawarrow (p)
else: drawdblarrow (gddTraceObjet p)
fi gddEnPlace
enddef;
beginfig(1);
d = 3;
A = Point(0,0);
B = Point(d,0);
C = Point(0,d);
C_A = Cercle(A,d);
C_B = Cercle(B,d);
E = IntersectionCercles(C_A,C_B);
C_E = Cercle(E,d);
F = IntersectionCercles(C_E,C_B);
% pour l’affichage de d
Ap = Addition(A,(0,-0.1));
Bp = Addition(B,(0,-0.1));
Sd = Segment(Ap,Bp);
trace Droite(A,B);
trace Droite(A,C);
drawoptions(withcolor DarkGrey);
doublefleche Sd;
doublefleche Segment(B,E);
gddLabel.bot(textext("$d$"),Milieu(Ap,Bp));
gddLabel.lft(textext("$d$"),Milieu(E,B));
drawoptions(withcolor Goldenrod);
trace gddTraceArcDeCercle(C_A,0,Pi/2);
trace gddTraceArcDeCercle(C_B,Pi/6,Pi);
trace gddTraceArcDeCercle(C_E,-1.2/3*Pi,Pi/6);
drawoptions(avecCrayon(0.7,IndianRed));
trace Droite(A,F);
trace Droite(A,E);
fleche Arc(A,1.5,0,Pi/6);
fleche Arc(A,1.2,Pi/6,Pi/3);
fleche Arc(A,1.,Pi/3,Pi/2);
gddLabel.rt(textext("$\frac{\pi}{6}$"),PointPolaire(1.5,Pi/12));
drawoptions();
marque.llft "A";
marque.lrt "B";
marque.bot "E";
marque.rt "F";
Fenetre(-0.5,-0.5,2.1*d,1.1*d);
endfig;
end.
Mots clés : géométriemp-geom2dcompasrègle