Auteur ou autrice : Maxime Chupin.
Mise en ligne le 25 janvier 2023
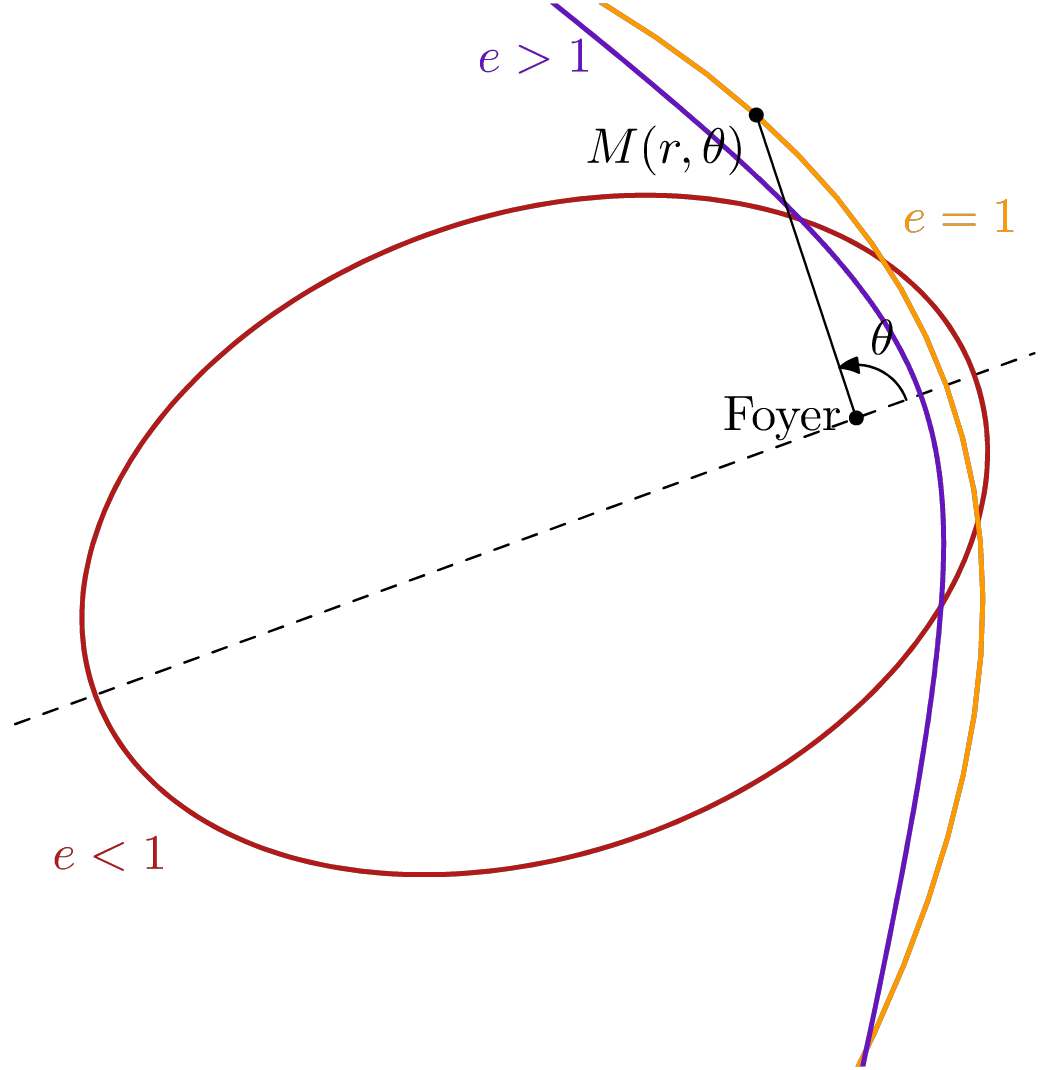
Voici un tracé des différents types de solutions du problème des deux corps en mécanique céleste.
En coordonnées polaires $(r,\theta)$, les solutions sont $$ r(\theta) = \frac{p}{1+e\cos\theta}.$$
Suivant la valeur de $e$ on a soit une ellipse, une parabole ou une hyperbole.
Code
%@Auteur : Maxime Chupin
%@Année : 2023
beginfig(1);
u:= 0.75cm;
a := 4.4u;
b:= 3u;
c := sqrt(a**2-b**2);
pair O;
O := (c,0);
rotation := 20;
path parabole, hyperbole;
for i:=-20 step 0.5 until 20:
if(i=-20):
parabole := u*(i,0.3*i**2-0.9);
else:
parabole := parabole--u*(i,0.3*i**2-0.9);
fi;
endfor;
p:=3.2;
e:=1.8;
debut := -120;
fin := 120;
for i:=debut step 0.5 until fin :
if(i=debut):
hyperbole := u*p/(1.0+e*cosd(i))*(cosd(i),sind(i));
else:
hyperbole := hyperbole -- u*p/(1.0+e*cosd(i))*(cosd(i),sind(i));
fi;
endfor;
pair M,Ox;
Ox := (5u,0);
M := u*(3,0.3*3**2-0.9) rotated 90 shifted O;
draw ((-10u,0)--(5u,0)) rotated rotation dashed evenly;
draw fullcircle xscaled 2a yscaled 2b rotated rotation withcolor (0.7,0.1,0.1)
withpen pencircle scaled 1pt;
draw parabole rotated 90 shifted O rotated rotation withcolor (1,0.6,0.)
withpen pencircle scaled 1pt;
draw hyperbole shifted (O-(0.5u,0)) rotated rotation withcolor (0.4,0.08,0.75)
withpen pencircle scaled 1pt;
draw (O--M) rotated rotation;
path arc[];
arc1 = (fullcircle rotated angle (Ox-O) scaled u shifted O cutafter (O--M))
rotated rotation;
drawarrow arc1;
label.urt(btex $\theta$ etex, point 1.5 of arc1);
dotlabel.llft(btex $M(r,\theta)$ etex, M rotated rotation);
dotlabel.lft(btex Foyer etex, O rotated rotation);
clip currentpicture to (unitsquare scaled 10u shifted (u*(-5,-5)));
label(btex $e<1$ etex, (-4u,-3u)) withcolor (0.7,0.1,0.1);
label(btex $e=1$ etex, (4u,3u)) withcolor (1,0.6,0.0);
label(btex $e>1$ etex, (0u,4.5u)) withcolor (0.4,0.08,0.75);
endfig;
end.