Auteur ou autrice : Maxime Chupin.
Mise en ligne le 25 janvier 2023
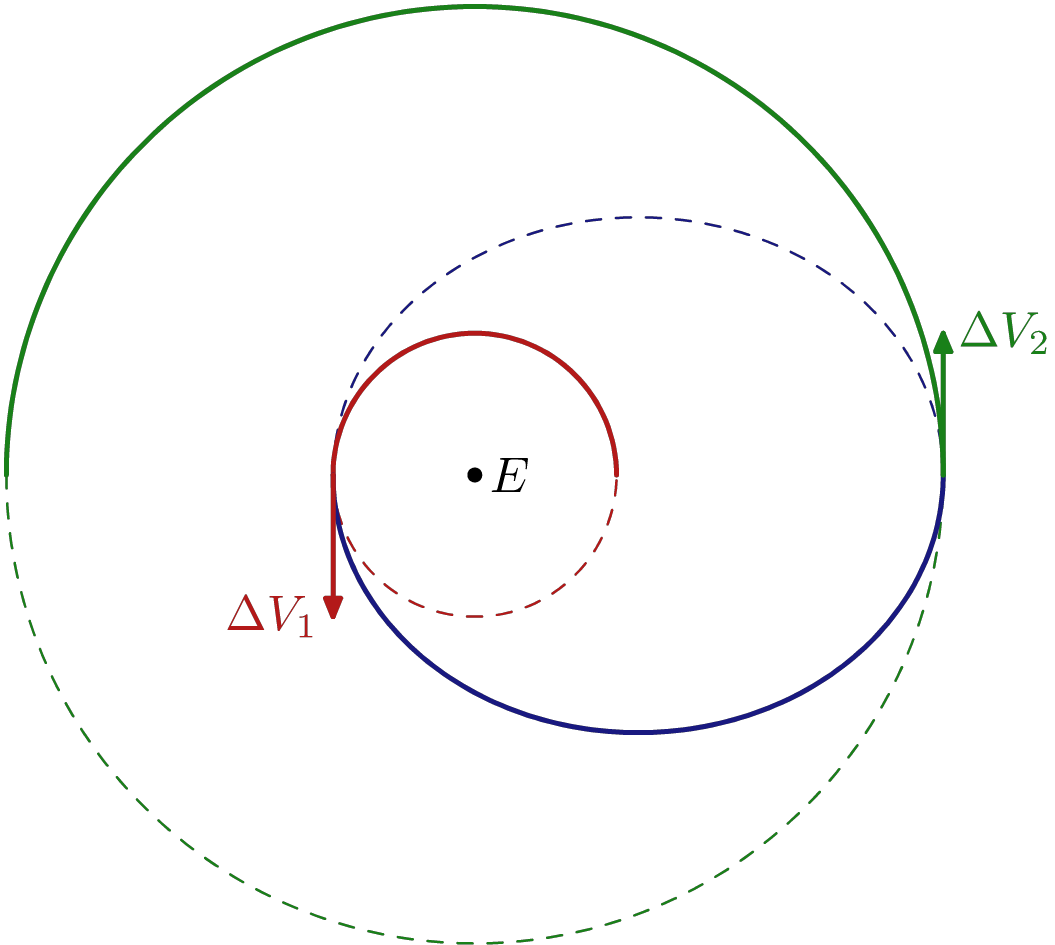
Une trajectoire ou transfert de Hohmann est une trajectoire qui permet de passer d’une orbite circulaire à une autre orbite circulaire située dans le même plan, en utilisant uniquement deux manœuvres impulsionnelles notées $\Delta V_1$ et $\Delta V_2$.
Code
%@Auteur : Maxime Chupin
%@Année : 2023
beginfig(0);
R:= 1cm; r1:=2*R; r2:= 6.61*R; a:= 0.5*(r1+r2);
e:= (r2-r1)/(r2+r1); b:= a*sqrt(1-e*e); c:= sqrt(a*a-b*b);
draw fullcircle scaled r1 withcolor (0.7,0.1,0.1) dashed evenly;
draw fullcircle scaled r2 withcolor (0.1,0.5,0.1) dashed evenly;
draw fullcircle xscaled a yscaled b shifted (0.5*c,0) withcolor (0.1,0.1,0.5) dashed evenly;
draw halfcircle scaled r1 withcolor (0.7,0.1,0.1) withpen pencircle scaled 1pt;
draw halfcircle xscaled a yscaled b rotated 180 shifted (0.5*c,0) withcolor (0.1,0.1,0.5) withpen pencircle scaled 1pt;
draw halfcircle scaled r2 withcolor (0.1,0.5,0.1) withpen pencircle scaled 1pt;
dotlabel.rt(btex $E$ etex,(0,0));
drawarrow (-r1,0)*0.5--(-r1,-r1)*0.5 withpen pencircle scaled 1pt withcolor (0.7,0.1,0.1);
drawarrow (r2,0)*0.5--(r2,r1)*0.5 withpen pencircle scaled 1pt withcolor (0.1,0.5,0.1);
label.lft(btex $\Delta V_{1}$ etex,(-0.5r1,-0.5r1)) withcolor (0.7,0.1,0.1);
label.rt(btex $\Delta V_{2}$ etex,(0.5r2,0.5r1)) withcolor (0.1,0.5,0.1);
endfig;
end.