Auteur ou autrice : Jean-Michel Sarlat.
Mise en ligne le 7 février 2023
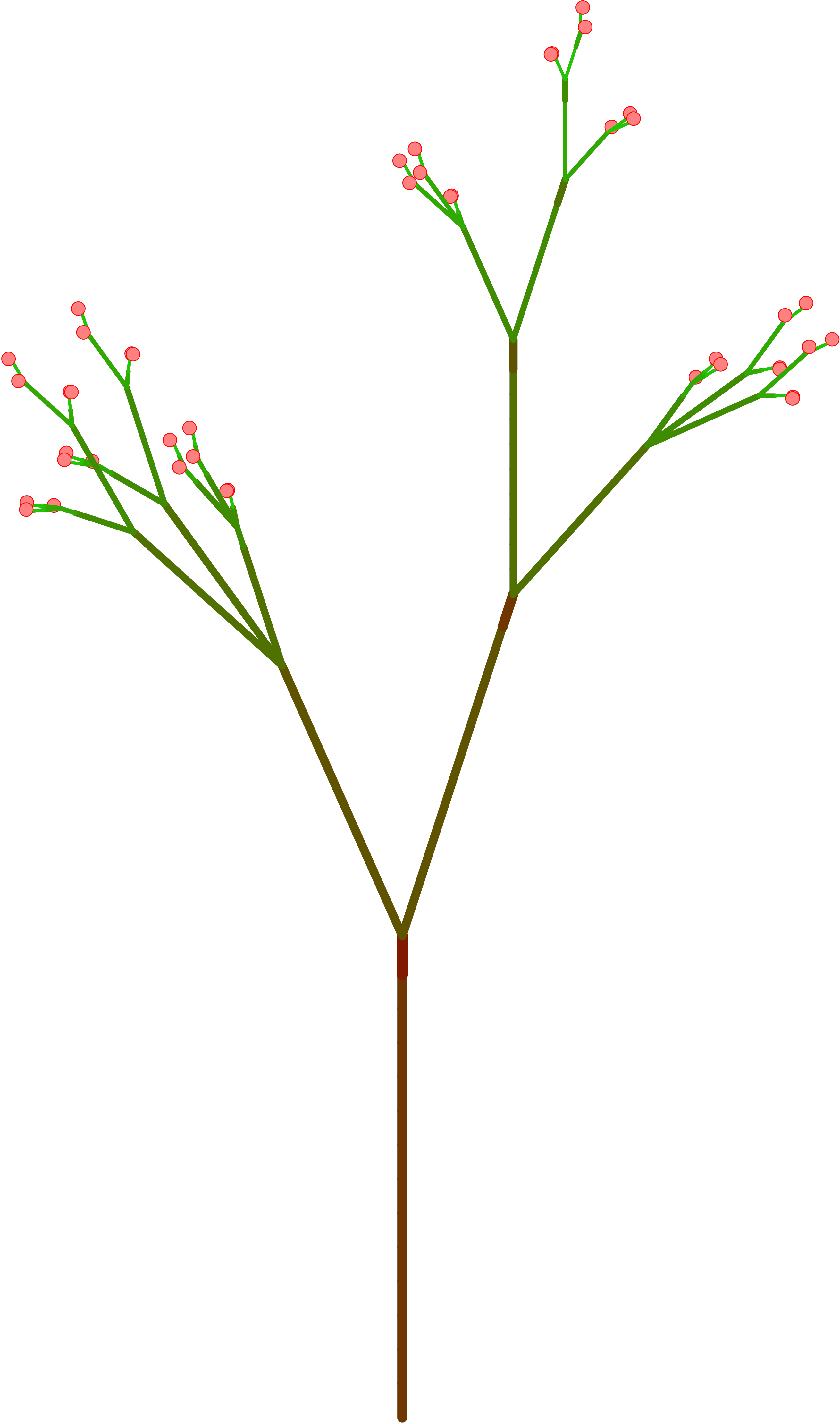
Arbres divers décrits par une tortue MetaPost (fichier tortue.mp). C'est une reprise des L-Systems (https://fr.wikipedia.org/wiki/L-Syst%C3%A8me) codés pour ImageMagick en perl (on les trouve dans la distibution de perlmagick).
L’exemple est extrait de la base MetaPost du site Syracuse : https://syracuse.eu.org/lab/bmp.
Code
%@Auteur : Jean-Michel Sarlat
%@Année : 2005
input tortue.mp;
numeric d,iter;
d = 6 ;
iter = 8;
color marron;
marron = (.5,.1,0);
def pas(expr x) = x * 1mm + .5mm enddef;
def epaisseur(expr x) = .3mm * x + .1mm enddef;
def couleur(expr x) = (x/iter)[green,marron] enddef;
vardef trace(expr a,b) =
draw a--b
withpen pencircle scaled e
withcolor c;
enddef;
%% lsys9
%% règle A => GS[---fMA][++++B]
%% règle B => C
%% règle C => GS[-fB][++A][++++A]
%% règle f => ' ' % seulement exécutée au terme
%% règle G => HS
%% règle H => HSS
vardef A (expr n,m) =
save h,e,c;
color c;
h := pas(m);
e := epaisseur(m);
c := couleur(m);
if m>0:
G(n,m-1);
avance(n,h,trace);
blop(n,n+1);
tourne(n+1,-3*d);
f(n+1,m-1);
retourne(n+1);
A(n+1,m-1);
blop(n,n+1);
tourne(n+1,4*d);
B(n+1,m-1);
fi
enddef;
vardef B (expr n,m) =
if m>0:
C(n,m-1);
fi
enddef;
vardef C (expr n,m) =
save h,e,c;
color c;
h := pas(m);
e := epaisseur(m);
c := couleur(m);
if m>0:
G(n,m-1);
avance(n,h,trace);
blop(n,n+1);
tourne(n+1,-1*d);
f(n+1,m-1);
B(n+1,m-1);
blop(n,n+1);
tourne(n+1,2*d);
A(n+1,m-1);
blop(n,n+1);
tourne(n+1,4*d);
A(n+1,m-1);
fi
enddef;
vardef G (expr n,m) =
save h,e,c;
color c;
h := pas(iter-n);
e := epaisseur(iter-n);
c := couleur(iter-n);
if m>0:
H(n,m-1);
avance(n,h,trace);
fi
enddef;
vardef H (expr n,m) =
save h,e,c;
color c;
h := pas(iter-n);
e := epaisseur(iter-n);
c := couleur(iter-n);
if m>0:
H(n,m-1);
avance(n,h,trace);
avance(n,h,trace);
fi
enddef;
vardef f (expr n,m) =
if m=0:
fill (fullcircle scaled 3mm) shifted tortue_xy[n] withcolor .5[red,white];
draw (fullcircle scaled 3mm) shifted tortue_xy[n] withcolor red;
fi
enddef;
beginfig(1);
tortue(1,0,0,90,1);
A(1,iter);
endfig;
end
% package tortue.mp
%% Les tables (chemin,point actuel,orientation,direction)
path tortue_p[];
pair tortue_xy[] ;
numeric tortue_m[];
numeric tortue_a[];
%% L'enregistrement d'une tortue (initialisation)
def tortue(expr n, x , y , a , m ) =
tortue_xy[n] := (x,y) ;
tortue_a[n] := a ;
tortue_m[n] := m ;
tortue_p[n] := (x,y);
enddef;
%% La tortue <n> se dédouble, <m> à cet instant se superpose à <n>
def blop(expr n,m) =
tortue(m,(xpart tortue_xy[n]),(ypart tortue_xy[n]),tortue_a[n],tortue_m[n]);
enddef;
%% La tortue tourne (sur place)
def tourne(expr n, a ) =
tortue_a[n] := tortue_a[n] + a * tortue_m[n];
enddef;
%% La tortue se retourne, sa gauche est notre droite !
def retourne(expr n ) =
tortue_m[n] := -tortue_m[n];
enddef;
%% La tortue avance d'une certaine distance et fait ce qu'on lui demande
vardef avance(expr n,l)(suffix m) =
pair position;
position = tortue_xy[n] + ((l,0) rotated tortue_a[n]);
m(tortue_xy[n],position);
tortue_xy[n] := position;
tortue_p[n] := tortue_p[n]--position;
enddef;
%% Remplissage du polygone circonscrit par le chemin de la tortue
vardef remplis(expr n,c) =
fill tortue_p[n]--cycle withcolor c;
enddef;
%% Une chose que la tortue peut faire en se déplaçant : laisser une trace !
vardef trace(expr a,b) =
draw a--b;
enddef;
