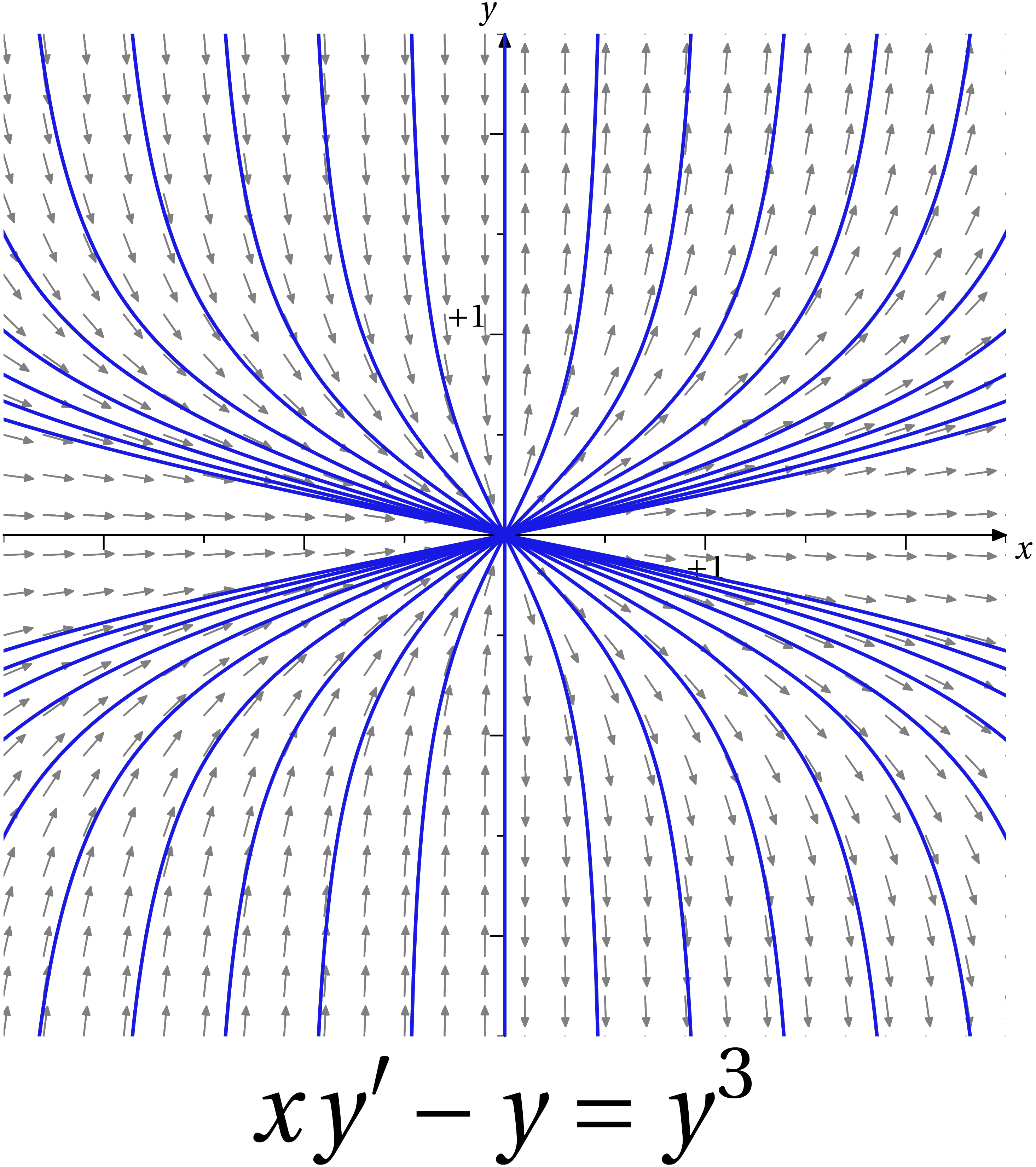
Tracé de solution d’une équation différentielle et du champ de vecteur associé (3)
Auteur ou autrice : Jean-Michel Sarlat.
Mise en ligne le 7 février 2023
Tracé de solutions d’une équation différentielle et du champ de vecteur associé.
Code
%@Auteur: Jean-Michel Sarlat
%@Année: 2005
input geometrie2d;
input courbes;
vardef fx(expr x) = a*x/sqrt(1+x*x) enddef;
vardef fy(expr x) = x enddef;
beginfig(1);
Repere(10,10,5,5,2,2);
Axes;
Debut;
Graduations;
Unites(1);
%% Champs de vecteurs
ahlength := 2.5;
vardef F(expr x,y) = (y**3+y)/x enddef;
ChampVecteurs(F,0.1,0.1,0.2,0.2,0.15,0.5white);
%% Courbes intégrales
for n = 0 upto 20:
a := (n/2) - 5;
trace Courbe(fx,fy,-2.5,2.5,50)
withpen pencircle scaled 1
withcolor (0.1,0.1,0.9);
endfor;
Fin;
Etiquette("$xy'-y=y^3$",3,(5,-0.7));
endfig;
end
Mots clés : mathématiqueséquation différentielleTeX
Cet exemple fait partie de la collection d’exemples Équations différentielles.
Fichiers
Télécharger l’archive complète
Fichiers auxiliaires
if unknown sh:
input fonctions;
fi;
if unknown Repere:
input reperes;
fi;
%
% Courbe paramtre
% -----------------------------------------------------------------------------
vardef Courbe(suffix fx)(suffix fy)(expr ti,tf,n) =
save fpas;
fpas := (tf-ti)/n;
(fx(ti),fy(ti)) for i=1 upto n: ..(fx(ti+i*fpas),fy(ti+i*fpas)) endfor
enddef;
%
% Reprsentation de fonction
% -----------------------------------------------------------------------------
vardef Representation(suffix f)(expr ti,tf,n) =
save fpas;
fpas := (tf-ti)/n;
(ti,f(ti)) for i=1 upto n: ..(ti+i*fpas,f(ti+i*fpas)) endfor
enddef;
%
% Courbe en polaire
% -----------------------------------------------------------------------------
vardef CourbeEnPolaires(suffix r)(expr ti,tf,n) =
save fpas,t;
fpas := (tf-ti)/n;
r(ti)*(cos(ti),sin(ti))
for i=1 upto n: hide(t:=ti+i*fpas) .. r(t)*(cos(t),sin(t)) endfor
enddef;
vardef ChampVecteurs(suffix f)(expr x,y,px,py,dx,couleur) =
for i = 0 upto (x - rXMIN)/px:
for j = 0 upto (y - rYMIN)/py:
drawarrow
(((0,0)--dx*unitvector((1,f(x-i*px,y-j*py))))
shifted (x-i*px,y-j*py)) gENPLACE
withcolor couleur;
endfor
for j = 0 upto (rYMAX - y)/py:
drawarrow
(((0,0)--dx*unitvector((1,f(x-i*px,y+j*py))))
shifted (x-i*px,y+j*py)) gENPLACE
withcolor couleur;
endfor
endfor
for i = 0 upto (rXMAX - x)/px:
for j = 0 upto (y - rYMIN)/py:
drawarrow
(((0,0)--dx*unitvector((1,f(x+i*px,y-j*py))))
shifted (x+i*px,y-j*px)) gENPLACE
withcolor couleur;
endfor
for j = 0 upto (rYMAX - y)/py:
drawarrow
(((0,0)--dx*unitvector((1,f(x+i*px,y+j*py))))
shifted (x+i*px,y+j*py)) gENPLACE
withcolor couleur;
endfor
endfor
enddef;
endinput;
numeric Pi;
numeric E;
Pi := 3.14159265;
E := 2.72828;
vardef sin(expr x) =
sind(x/Pi*180)
enddef;
vardef cos(expr x) =
cosd(x/Pi*180)
enddef;
vardef tan(expr x) =
sin(x)/cos(x)
enddef;
vardef exp(expr x) =
E**x
enddef;
vardef ch(expr x) = (E**x + E**(-x))/2 enddef;
vardef sh(expr x) = (E**x - E**(-x))/2 enddef;
vardef th(expr x) = (E**(2*x) - 1)/(E**(2*x) + 1) enddef;
endinput
input labels;
string ogT[];
numeric ogTA[], ogTB[], ogTC[], ogTD[], ogTE[], ogTF[];
numeric ogt, gTRD, gU, gPR;
% ogt est le compteur des objets graphiques crs.
ogt := 0;
% Paramtre utilis pour le trac des droites. Il fixe la longueur du segment
% trac en fonction de la longueur du bipoint qui dfinit la droite.
gTRD := 5;
% gU est l'unit de base, ici le cm.
gU := 1cm;
% gENPLACE est la transformation qui place les objets ... en premier.
def gENPLACE = scaled gU enddef;
% diamtre des cercles marquant les points
gPR := 2;
% Point -----------------------------------------------------------------------
vardef Point (expr a,b) =
ogT[incr ogt] = "point";
ogTA[ogt] = a; ogTB[ogt] = b;
ogt
enddef;
% Vecteur ---------------------------------------------------------------------
vardef Vecteur (expr a,b) =
ogT[incr ogt] = "vecteur";
ogTA[ogt] = a; ogTB[ogt] = b;
ogt
enddef;
% Droite ----------------------------------------------------------------------
vardef Droite (expr a,b) =
ogT[incr ogt] = "droite";
ogTA[ogt] = a; ogTB[ogt] = b;
ogt
enddef;
% Segment ---------------------------------------------------------------------
vardef Segment (expr a,b) =
ogT[incr ogt] = "segment";
ogTA[ogt] = a; ogTB[ogt] = b;
ogt
enddef;
% Triangle --------------------------------------------------------------------
vardef Triangle (expr a,b,c) =
ogT[incr ogt] = "triangle";
ogTA[ogt] = a; ogTB[ogt] = b; ogTC[ogt] = c;
ogt
enddef;
% Cercle ----------------------------------------------------------------------
vardef Cercle (expr a,b) =
ogT[incr ogt] = "cercle";
ogTA[ogt] = a; ogTB[ogt] = b;
ogt
enddef;
% Quadrilatre complet --------------------------------------------------------
vardef QComplet (expr a,b,c,d,e) =
save p,r; pair p, numeric r;
ogT[incr ogt] = "qcomplet"; r = ogt;
ogTA[ogt] = a; ogTB[ogt] = b; ogTC[ogt] = c;
ogTD[r] = Point_(d [_Point(a), _Point(b)]);
ogTE[r] = Point_(e [_Point(b), _Point(c)]);
p = whatever [ _Point(a), _Point(c) ];
p = whatever [ _Point(ogTD[r]), _Point(ogTE[r]) ];
ogTF[r] = Point_(p);
r
enddef;
% Isobarycentre d'une liste de points <t> .....................................
vardef IsoBarycentre (text t) =
save x,y,n;
x := 0; y := 0; n := 0;
for p_ = t:
x := x + ogTA[p_];
y := y + ogTB[p_];
n := n + 1 ;
endfor;
if n>0: Point ((1/n)*x,(1/n)*y) fi
enddef;
% Barycentre des points <a> et <b>, <b> est affect du poids x, <a> du poids 1-x
vardef Barycentre (expr a,b,x) =
save p; pair p;
p = x [ _Point(a), _Point(b)];
Point_(p)
enddef;
% Milieu du segement <a> ......................................................
vardef Milieu (expr a) =
IsoBarycentre(ogTA[a],ogTB[a])
enddef;
% Mdiatrice du segment <a> ...................................................
vardef Mediatrice (expr a) =
save p,q; pair q;
p = Milieu(a);
q = _Point(p) + (_Vecteur(a) rotated 90);
Droite(p,Point_(q))
enddef;
% Bissectrice de l'angle de sommet <b> limit par les points <a> et <c> .......
vardef Bissectrice (expr a,b,c) =
save p,q,r,t; pair p,q,r,t;
q = _Point(b);
p = q + unitvector(_Point(a) - q);
r = q + unitvector(_Point(c) - q);
t - p = whatever * (q - p) rotated 90;
t - r = whatever * (q - r) rotated 90;
Droite(b,Point_(t))
enddef;
% Perpendiculaire la droite <b> passant par <a> .............................
vardef Perpendiculaire (expr a,b) =
Droite(a,Point_(_Point(a) + (_Vecteur(b) rotated 90)))
enddef;
% Intersection des droites <a> et <b> .........................................
vardef Intersection (expr a,b) =
save p; pair p;
p = whatever [ _Point(ogTA[a]), _Point(ogTB[a]) ];
p = whatever [ _Point(ogTA[b]), _Point(ogTB[b]) ];
Point_(p)
enddef;
% Projection du point <a> sur la droite <b> ...................................
vardef Projection (expr a,b) =
Point_(_Projection(a,b))
enddef;
% Orthocentre du triangle <t> .................................................
vardef Orthocentre (expr t) =
Intersection(
Perpendiculaire(PointDe(t,1),Droite(PointDe(t,2),PointDe(t,3))),
Perpendiculaire(PointDe(t,2),Droite(PointDe(t,3),PointDe(t,1)))
)
enddef;
% Symtrique de <a> par rapport au point ou la droite <b> ...................
vardef Symetrique (expr a,b) =
if ogT[b] = "point":
Point_(2 [_Point(a), _Point(b))
else:
Point_(_Point(a) reflectedabout (_Point(ogTA[b]),_Point(ogTB[b])))
fi
enddef;
% Distance entre le point <a> et le point/droite <b> ..........................
vardef Distance (expr a,b) =
if ogT[b] = "droite":
abs(_Point(a) - _Projection(a,b))
else:
abs(_Point(a) - _Point(b))
fi
enddef;
% Cercle circonscrit au triangle <a> ..........................................
vardef CercleCirconscrit (expr a) =
save p,r;
p = Intersection(
Mediatrice(Segment(ogTA[a],ogTB[a])),
Mediatrice(Segment(ogTB[a],ogTC[a]))
);
r = Distance(p,ogTA[a]);
Cercle(p,r)
enddef;
% Centre du cercle <c> ........................................................
vardef Centre(expr a) =
ogTA[a]
enddef;
% Rayon du cercle <c> .........................................................
vardef Rayon(expr a) =
ogTB[a]
enddef;
%% ============================================================================
%% objets Point, Vecteur et pairs au sens de METAPOST.
%% Passage des uns aux autres ...
%% ============================================================================
def _Point(expr a) = (ogTA[a],ogTB[a]) enddef;
def Point_(expr p) = Point(xpart p,ypart p) enddef;
let ptoPoint = Point_;
def _Vecteur(expr a) = (_Point(ogTB[a]) - _Point(ogTA[a])) enddef;
vardef _Projection (expr a,b) = save p; pair p;
p = _Point(a) + whatever * _Vecteur(b) rotated 90;
p = whatever [ _Point(ogTA[b]), _Point(ogTB[b]) ];
p enddef;
%% ----------------------------------------------------------------------------
def PointDe(expr a,b) =
if b = 1:
ogTA[a]
elseif b = 2:
ogTB[a]
elseif b = 3:
ogTC[a]
elseif b = 4:
ogTD[a]
elseif b = 5:
ogTE[a]
elseif b = 6:
ogTF[a]
fi
enddef;
def Lieu expr o =
if ogT[o] = "triangle":
_Point(ogTA[o])--_Point(ogTB[o])--_Point(ogTC[o])--cycle
elseif ogT[o] = "droite":
(gTRD [ _Point(ogTA[o]), _Point(ogTB[o]) ]) --
(gTRD [ _Point(ogTB[o]), _Point(ogTA[o]) ])
elseif ogT[o] = "segment":
_Point(ogTA[o]) -- _Point(ogTB[o])
elseif ogT[o] = "cercle":
fullcircle scaled (ogTB[o]*2) shifted _Point(ogTA[o])
elseif ogT[o] = "qcomplet":
_Point(ogTA[o]) -- _Point(ogTB[o]) -- _Point(ogTE[o]) --
_Point(ogTD[o]) -- _Point(ogTA[o]) -- _Point(ogTC[o]) --
_Point(ogTE[o])
fi
enddef;
def _pointe(expr p) =
fill (fullcircle scaled gPR) shifted (p gENPLACE) withcolor white;
draw (fullcircle scaled gPR) shifted (p gENPLACE)
enddef;
def trace expr p = if path p: draw p else: draw (Lieu p) fi gENPLACE enddef;
def remplis expr p = if path p: fill p else: fill (Lieu p) fi gENPLACE enddef;
def pointe expr p = if pair p: _pointe(p) else: _pointe(_Point(p)) fi enddef;
vardef marque.@# expr p =
pointe(scantokens p);
label.@#(lTEX(p),_Point(scantokens p) gENPLACE);
enddef;
def SigneOrtho(expr a,b,c,x) =
(_Point(b) + x * unitvector(_Point(a)-_Point(b)))
-- (_Point(b) + x * unitvector(_Point(a) - _Point(b))
+ x * unitvector(_Point(c) - _Point(b)))
-- (_Point(b) + x * unitvector(_Point(c) - _Point(b)))
enddef;
%% ----------------------------------------------------------------------------
def Fenetre(expr xg,yg,xd,yd) =
gpXG := xg;
gpYG := yg;
gpXD := xd;
gpYD := yd;
extra_endfig := "_fenetre;" & extra_endfig;
enddef;
def _fenetre =
clip currentpicture to
((gpXG,gpYG)--(gpXG,gpYD)--(gpXD,gpYD)--(gpXD,gpYG)--cycle) scaled gENPLECE
enddef;
endinput
lFOURIER := 1;
string lSTRING[];
lSTRING[0] = "alpha";
lSTRING[1] = "beta";
lSTRING[2] = "gamma";
lSTRING[3] = "delta";
lSNB = 3;
vardef scanchaine_label(expr s) =
save d,m,f,c,l,flag,i; string d,m,f,c;
d := ""; m := ""; f := "";
l = length(s); flag := 0;
for i:=0 upto l:
c := substring (i,i+1) of s;
if c = "'":
f := f & c; flag := 2;
elseif c = "_":
flag := 1;
else:
if flag = 0:
d := d & c
else:
m := m & c
fi;
fi
endfor;
for i:=0 upto lSNB:
if d = lSTRING[i]: d := "\" & d fi
endfor;
d := d & "_{" & m & "}" & f;
d
enddef;
vardef lTEX primary s =
write "verbatimtex" to "mptextmp.mp";
write "%&latex" to "mptextmp.mp";
write "\documentclass{article}" to "mptextmp.mp";
if lFOURIER=1: write "\usepackage{fourier}" to "mptextmp.mp" fi;
write "\begin{document}" to "mptextmp.mp";
write "etex" to "mptextmp.mp";
write "btex $"& scanchaine_label(s) &"$ etex" to "mptextmp.mp";
write EOF to "mptextmp.mp";
scantokens "input mptextmp"
enddef;
vardef TEX primary s =
write "verbatimtex" to "mptextmp.mp";
write "%&latex" to "mptextmp.mp";
write "\documentclass{article}" to "mptextmp.mp";
if lFOURIER=1: write "\usepackage{fourier}" to "mptextmp.mp" fi;
write "\usepackage{amsmath}" to "mptextmp.mp";
write "\everymath{\displaystyle}" to "mptextmp.mp";
write "\begin{document}" to "mptextmp.mp";
write "etex" to "mptextmp.mp";
write "btex "& s &" etex" to "mptextmp.mp";
write EOF to "mptextmp.mp";
scantokens "input mptextmp"
enddef;
endinput
picture rSAVEPICT;
def Repere(expr l,h,ox,oy,ux,uy) =
def gENPLACE = xscaled ux yscaled uy shifted (ox,oy) scaled gU enddef;
rLARGEUR := l; rHAUTEUR = h;
rXMIN := - ox / ux; rXMAX := rXMIN + l / ux;
rYMIN := - oy / uy; rYMAX := rYMIN + h / uy;
rUX := ux; rUY := uy;
enddef;
def Debut =
rSAVEPICT := currentpicture; currentpicture := nullpicture;
enddef;
def Fin =
clip currentpicture to
( (0,0)--(rLARGEUR,0)--(rLARGEUR,rHAUTEUR)--(0,rHAUTEUR)--cycle)
scaled gU;
addto rSAVEPICT also currentpicture;
currentpicture := rSAVEPICT;
def gENPLACE = scaled gU enddef;
enddef;
def Axes =
drawarrow ((rXMIN,0)--(rXMAX,0)) gENPLACE;
drawarrow ((0,rYMIN)--(0,rYMAX)) gENPLACE;
label.lrt(TEX("$x$"),(rXMAX,0) gENPLACE);
label.ulft(TEX("$y$"),(0,rYMAX) gENPLACE);
enddef;
vardef Graduations =
xmin = floor(rXMIN); xmax = floor(rXMAX) + 1;
ymin = floor(rYMIN); ymax = floor(rYMAX) + 1;
SequenceTirets((xmin,0),(1,0),(0,-4),xmax-xmin+1);
SequenceTirets((xmin+0.5,0),(1,0),(0,-2),xmax-xmin);
SequenceTirets((0,ymin),(0,1),(-4,0),ymax-ymin+1);
SequenceTirets((0,ymin+0.5),(0,1),(-2,0),ymax-ymin);
enddef;
%
% SequenceTirets
% ------------------------------------------------------------------------------
vardef SequenceTirets(expr o,p,t,n) text a=
save ot; pair ot; ot := o gENPLACE;
for i:=1 upto n:
% tiret
draw ot -- (ot shifted t) a;
% avancement
ot := (o + i*p) gENPLACE;
endfor
enddef;
vardef Unites(expr t) =
if t=1:
label.bot(TEX("$+1$"),(1,-(3/gU/rUY)) gENPLACE);
label.ulft(TEX("$+1$"),(-(3/gU/rUX),1) gENPLACE);
fi
enddef;
vardef Etiquette.@#(expr s,t,p) = label.@#(TEX(s) scaled t,p gENPLACE) enddef;
endinput